Pascal’s Triangle and Chinese
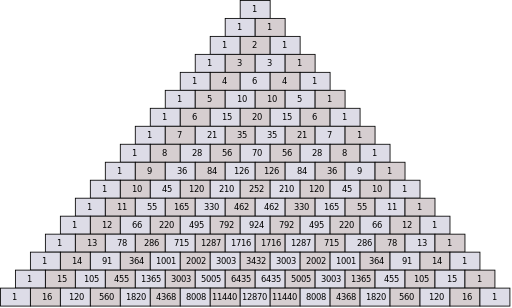
This is one of those blog posts where I take two seemingly very different topics and connect them to China or Chinese. This time it’s about Pascal’s Triangle, one of my favorite mathematical concepts. In case you’re unfamiliar with Pascal’s Triangle, here are some images from Wikimedia Commons that nicely illustrate the principle:
Here’s the China connection (via Wikipedia):
> The set of numbers that form Pascal’s triangle were known before Pascal. However, Pascal developed many uses of it and was the first one to organize all the information together in his treatise, Traité du triangle arithmétique (1653). The numbers originally arose from Hindu studies of combinatorics and binomial numbers and the Greeks’ study of figurate numbers.
> […]
> In 13th century, Yang Hui [杨辉] (1238–1298) presented the arithmetic triangle that is the same as Pascal’s triangle. Pascal’s triangle is called Yang Hui’s triangle in China. The “Yang Hui’s triangle” was known in China in the early 11th century by the Chinese mathematician Jia Xian [贾宪] (1010–1070).
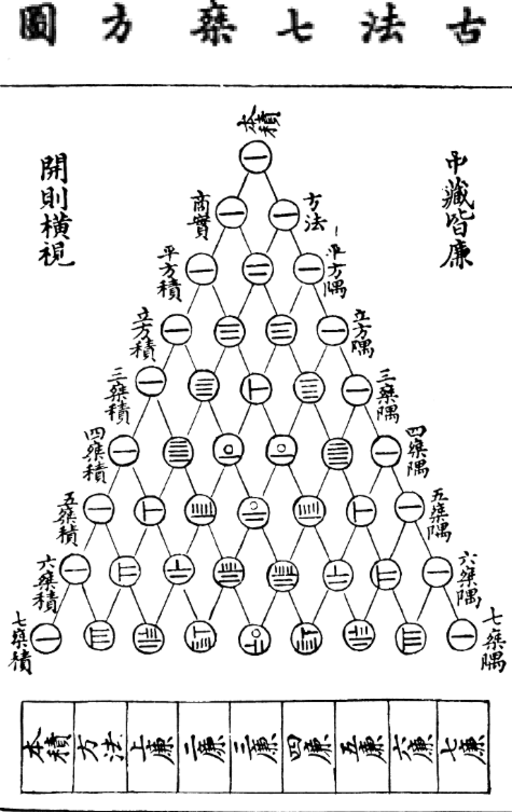
Yang Hui’s diagram contains some interesting-looking numbers. Check it out:
Compare that to Pascal’s triangle above. What’s up with these Chinese numbers? You can follow the upper-right to lower-left diagonal (one row in) to follow the numbers 1-8. You get this:
1. 一
2. 二
3. 三
4. 亖
5. [no Unicode symbol for this one; it’s just 亖 + 一 (vertical)]
6. ᅡ
7. ᅣ
8. [no Unicode symbol for this one; it’s just ᅵ + 三 (horizontal)]
You can gather that 10 is 으 [a symbol I borrowed from Korean Hangul for the purposes of this post], which also looks like “10” turned sideways. 20, though, is 〇二 [except with the 〇 sitting on top of the 二], and so on.
I’ve written before on Chinese number character variants, but these are different from those. The numbers look similar to Suzhou numerals and Shang oracle numerals, but are still a bit different from both. I’m curious if anyone out there know more about these numbers? The diagram supposedly dates to 1303 (more info on Wikimedia Commons).
There’s another personal connection between me and Pascal’s Triangle. As part of my research for AllSet Learning, I make use of basic set theory and higher-level Venn diagrams. Considering that in a Venn diagram, by definition, all possible logical relations between sets must be represented, it can get quite tricky to draw these things when you delve into Venn diagrams with higher numbers of sets (more than 3). But how do you know how many overlapping regions there are in the Venn diagrams as the numbers of sets increase? Pascal’s triangle.
(BTW, some of the research we’re doing now at AllSet Learning could make use of interns with a foundation in statistics, mathematics, or computer science. If that’s you, get in touch! More on AllSet Learning’s interns here.)


These are so called ‘counting rods,’ and there ARE Unicode characters for those!
1.
Uh, oh. Preview of my previous comment awaiting moderation suggests that your site might have troubles with Unicode characters outside the Basic Multilingual Plane (those with numbers over u+FFFF), and counting rods start at u+1D360. But don’t worry, very few websites on the Internet support Unicode correctly as of today (sic!).
Handy reference: http://www.unicode.org/charts/PDF/U1D360.pdf
I just taught this a few weeks ago as part of binomial expansion. The Wikipedia 古法七乘方圖Yanghui triangle was the handout, and figuring out the numbering system was part of the activity.
I can’t find the source now, but during my research I read that at some point an original Chinese text (by Jia Xian?) was lost and then re-imported back to China from Korea. This might explain why the 10 symbol looks like hangul. I’d be interested to know more about this though.
I don’t think the 0 has anything to do with Korean. One has to be able to set it apart from the 一 somehow.
I think they look a lot like babylonean numerals more than anything.
http://en.wikipedia.org/wiki/Babylonian_numerals
Main similarities:
1. They kind of just write out the strokes/cuneiforms till they get to ten
2. They then rotate the strokes 90 degrees. A horizintal stroke represents 10 two 20 and so on.
3. These can be combined
The Chinese seem to have a slightly more sophisticated way of dividing the numbers once more into 5-ers, tough. This is a few hundered years later, but it seems to be along the same lines.
Sorry, I meant thousands not hundereds.
你好John, 酷!你也知道”Chinese Remainder Theorem?” 很有用(RSA public key cryptography):
http://en.wikipedia.org/wiki/Chinese_remainder_theorem
Bill
What about the origins of the tally keeping character 正? I’ve always wondered about that.
I don’t know, but I would guess that it’s a combination of (1) being a common character, (2) having 5 very clear separate strokes, without bends or hooks, and (3) easy to write.
Strange… These look to be Zhou dynasty bamboo (rod) numerals, but I have no idea why they’d appear on a document dated 1303 (unless they were still in use as a classic-type numeral for a several centuries). Cool post!
(Spoiler alert)
Readers interested in Chinese numerals might enjoy episode 2 of Sherlock, the BBC TV drama that puts the detective into the present age. Hangzhou/Suzhou numerals play an important part.